
| James Dagg has a BSME in mechanical engineering and a MSE in Applied Mechanics from the University of Michigan. He has been involved in the development of engineering software at Altair Engineering for the last 15+ years. He can only ride cycles with two or more wheels |  |
For fun, James offered to analyze some of the static and dynamic behaviours of the unicycle. The first test that the actual frame was subjected to was a static sag test. In the static sag test, the frame is supported at both ends while laying horizontally above the ground. James' analysis conservatively predicts that the center should sag about 1.24 meters. In the actual test, it sagged a little over a meter before touching the ground in the middle.

Another computer simulation estimates that the theoretical maximum static weight that the frame can withstand at the top is about 500 pounds before it buckles. Of course while Sem is pedaling, the frame will be flexing and vibrating so the safe operating load is less. Sem weighs in at 145 pounds so unless he has a really large meal before riding, he should be ok. The animations below show the predicted buckling behaviour of the frame when more than 500 pounds are applied to the top:
| View from rider's seat of first global buckling mode |
|---|
| Side view of first global buckling mode |
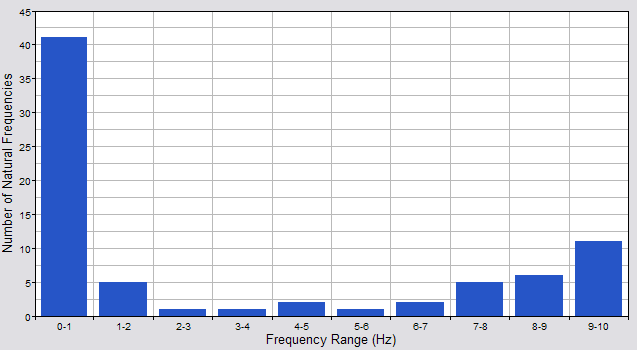
Such a tall thin structure is sure to have interesting vibrational characteristics-- especially with Sem spinning the crank at the top. James ran a modal analysis of the structure including the rider to compute the natural frequencies of the system. The chart below shows the distribution of the first 75 natural frequencies. As you can see, there are over 40 modes below 1 Hz!
The animation shows several of the interesting natural vibration patterns, or mode shapes of the frame. The magnitude of the modes has been exagerated to make them more clear-- the structure never actually bends this much. In fact, at any given time, the total vibrational state of the frame is really a combination of many such modes acting simultaneously to various degrees.